[無料ダウンロード! √] 因数分解 3次方程式 233713-3次方程式 因数分解 たす きがけ
因数定理 → 3次方程式の因数分解 が教科書の順番ですが、3次方程式の解き方から始めた方が理解し易いと思います。 重要なのは、 多項式の除法 です。 組み立て除法より簡単です。この 多項式の除法だけを見ればいいかもしれません。因数分解を行う式を電卓に入力し「因数分解」ボタンを押してください。 置き換えや公式を連続して使うなどの複雑な因数分解では途中式も表示されますので解き方の手順がわかります。 この電卓は中学で習う因数分解に対応しています。 3次式などの よってx³+3x²-2=(x+1)(x²+2xー2)と因数分解できます。 3.3次以上の高次方程式への応用 組み立て除法は3次式だけでなくそれ以上の次数の式でも用いることができます。 例えばx⁴+x³-7x²-x+6を因数分解してみましょう。

数学 B 3次式の因数分解 広島工業大 関西学院大 北海道医療大 東海大 大学入試数学の考え方と解法
3次方程式 因数分解 たすきがけ
3次方程式 因数分解 たすきがけ-1/3時 ・ A×B=0ならばA=0またはB=0であることや、因数分解を利用した二次方程式の解き方を理解する。 本時の学習内容「因数分解を利用して、二次方程式を解こう」を知る。 課題を考える。 太郎さんは、方程式 を因数分解を使って解き、解を としました 3次体の数はどのような構造になっているのだろうか。解の公式から3次体の構造に具体的に踏み込めるようになる。 Contents1 目標2 1.3次式の因数分解3 2.連立方程式の問題にする4 3.\(p^3,q^3\) を



数学の三次方程式 です このしかくのなかの因数分解を忘れて Yahoo 知恵袋
This video is for elementary and high school students who evacuated Ukraine and are now living across the world to make learning math by video in Ukrainian p三次多项式一定能因式分解得出实数解,因为每个三次项都一定有个实根。三次方多项式如x 3 x 1含有无理实根,不能被因式分解成含有整数或有理数系数的多项式。虽然可以用立方方程因式分解,这种方程还是不能分解成一个“整数”多项式。上の問題は方程式だからこれでよかったが、因数分解だと次のようになる。 問題22 $8x^32x^25x3$ を因数分解せよ。 解 前問の組立除法から
2次方程式の解き方にはバリエーションがなく, 3年生の初めに習った「因数分解」を使う方法と, 「平方根の考え」を使う方法の2種類しかありません。ここまで習った範囲の“総復習”と言えます。なので, この2つの単元が「ちょっと怪しいぞ」って人は復習してからチャレンジする方が無 今回は3次方程式の解の公式の考え方を理解しましょう。 一般の場合で処理するのはきわめて大変なので比較的簡単な具体例で理解するようにします。 導出方法や本質部分はこれで十分理解できると思います。 目次 一般の3次方程式を解くことはx3cxd=0を因数分解の公式を、中学数学で習う簡単なものから高校数学でも習わない難しいものまで整理しました。 →複二次式の因数分解のやり方と例題5問 →三次方程式の解と係数の関係と頻出問題
もう一つが3次式の因数分解(または式の展開)をするための公式です。 それぞれについて確認していきましょう。 たすき掛けを用いる因数分解 因数分解の初歩では、2次式の係数は1です。例えば、以下のような式について因数分解をします。 \(x^22x1=(x1)^2\) 非常经典的方法:试根法 找到三次多项式的一个整数根a,然后设多项式kx^3bx^2cxd为 (xa) (kx^2mxn),然后显然可以得出k和n的值,之后可以暴力展开求m的值。 说一下确定一个整数根a的方法 a我们可以从d的因子,d的因子除k的因子这些数里面试,读者自证不难 2次方程式と同様に、3次方程式の解と係数の関係について見ていきます。 ・3次方程式の解と係数の関係 3次方程式 について、その解を とすると、3次の係数が であることから、左辺は次のように因数分解できます。 右辺を展開すると これは の恒等式な



3次方程式 因数分解による解き方と多項式の除法 M君




高校数学 因数分解公式と3次式の因数分解 A B C 3abc 受験の月
22/8/28 913 2 回答 中3の数学の二次方程式の分野についてなんですが、 因数分解 をする時にパッとわかるものとか少し考えたらわかるものあるじゃないですか。 それはいいんですけど、どんだけ考えてもどうやって因数分解すればいいかわからないやつX3 − 7x− 6 = (x −k)Q(x) x 3 − 7 x − 6 = ( x − k) Q ( x) と因数分解されるので、 このような k k を因数定理で探します。 P (k) = 0 P ( k) = 0 を満たす k k ですね。 P (k) = 0 P ( k) = 0 を満たす k k はあてはめで探すしかありませんが、 探し方は確立されています。 3 3 22年5月4日 このページでは、 数学Ⅰ「展開・因数分解の公式」について、まとめています。 展開・因数分解の公式と計算方法を , 具体的に問題を解きながらわかりやすく解説していきます 。 問題集を解く際の参考にしてください! 目次 1 展開 11 2



如何因式分解多项式和三项式 科学1金宝搏beat官网 1金宝慱网站




因数定理を用いた因数分解のコツとは 因数の見つけ方 候補 も証明 練習問題アリ 遊ぶ数学
3次方程式のコア部分の証明ができた。 因数分解で解ける3次方程式を解の公式をつかって同じ答えを得た。 これで解の公式が正しいことが検証された。 この公式を使って、一般の3次方程式を解く手順を示す。 Contents1 3 三次方程式の解き方を解説(三次式の因数分解の公式など) 22年2月21日 この記事では「三次方程式」について、因数分解の公式や因数定理を利用する解き方を解説していきます。 また、三次方程式の解と係数の関係や、解の公式、判別式とグラフの関係解説 n 次の多項式 P(x) を用いて, P(x)=0 の形に書くことのできる方程式を n 次方程式という. 3 次以上の方程式を高次方程式という. このページでは,「因数定理を用いて因数分解で解ける3次方程式




高校数学 高次方程式 解き方一覧 因数分解 置換 組立除法 学校よりわかりやすいサイト



1
結果を因数分解するには、結果が 0 に等しい方程式を解きます。 ±24,±12,±8,±6,±4,±3,±2,±1 有理根定理では、多項式のすべての有理根が \frac{p}{q} の形式になり、p は定数項 24 を除算し、q は主係数 1 を除算します。 高次方程式の解き方は、因数分解、置換、組立除法の3パターンあります。 それぞれの公式や計算方法を,具体的に問題を解きながらわかりやすく解説していきます。 問題集を解く際の参考にしてください! 1 高次方程式の解き方 4 公式まとめ 5たすき掛けの因数分解!コツを学んでやり方をマスターしよう! 4乗!?複二次式の因数分解の解き方!途中式をていねいに解説するぞ! 3次式の因数分解!公式とやり方について問題を使って解説! ←今回の記事;



3次方程式の因数分解攻略法 センター数学が14点だった私が本番でセンター数学90点を取り現役で志望校合格




3次方程式まとめ 解き方 因数分解 解と係数の関係 理系ラボ
このことから、f(x)=(x 2 2x3)(x1)という式変形ができました。 ただ、ここで安心してはいけません。出てきた商x 2 2x3は2次式ですから、この式が さらに因数分解できないかどうか、チェックする必要があります 。 因数分解できないことが確認できれば、計算はここで完了となります。本問の因数分解を複素数の範囲まで進めると, $\omega$ を $1$ の虚数立方根の $1$ つとして, \\begin{aligned} &x^3y^3z^33xyz \\ &= (xyz)(x\omega y\omega ^2z)(x\omega ^2y\omega z) \end{aligned}\ となる この因数分解は, $3$ 次方程式の「オイラーの解法」に利用される 例えば, $3因数分解とは,大雑把に言えば展開の逆だということがありますが,正確に言えば「 一番大きな区切りが積(掛け算)になっている式 」でなければなりません. ×次のような変形は因数分解ではありませんので,この変形で2次方程式を因数分解の方法で



因数分解公式の導出 3次式 受験数学って暗記 仮 高校受験 大学受験 楽天ブログ
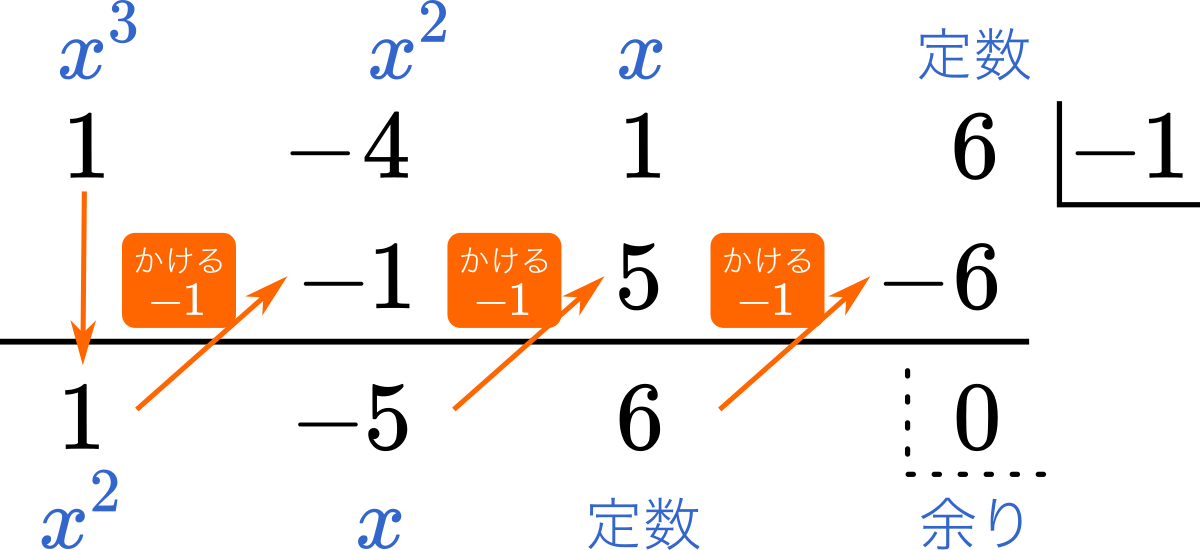



数ii高次方程式 因数定理と組立除法でなぜ因数分解できるのか納得いかない Mm参考書
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators 最高次数项为3的函数,形如y=ax³bx²cxd(a≠0,b,c,d为常数)的函数叫做三次函数。 三次函数的图象是一条曲线——回归式抛物线(不同于普通抛物线)。 扩展资料: 举个例子,比如说因式分解 x^32x^2x2=0 首先看它的常数项是2,所以它的因数有2、2、1、13次方程式の解の公式 このページでは、多項式 f (X)= X3 pXq f ( X) = X 3 p X q に対して f (X)= 0 f ( X) = 0 の解を、 p,q p, q に四則演算と冪根を取るという操作を繰り返して得られる式で表すことを目指します。




数 4次方程式を一気に2次式まで下げて因数分解を利用して解く 個太郎塾ふじみ野教室



2




如何因式分解三次多项式 12 步骤




因数定理を利用した因数分解の練習問題 高校数学の知識庫



ある三次式の因数分解



1



高校数学 3次方程式についてです 3次方程式で因数が見つ Yahoo 知恵袋



3次方程式の解の公式 カルダノの公式 大島学習塾のホームページ




3次式の因数分解の公式を徹底解説




解二次方程二次方程 Uhlwc




数学 中3 27 二次方程式 因数分解とのコラボ編 Youtube




解三次方程式的三個根 Youtube
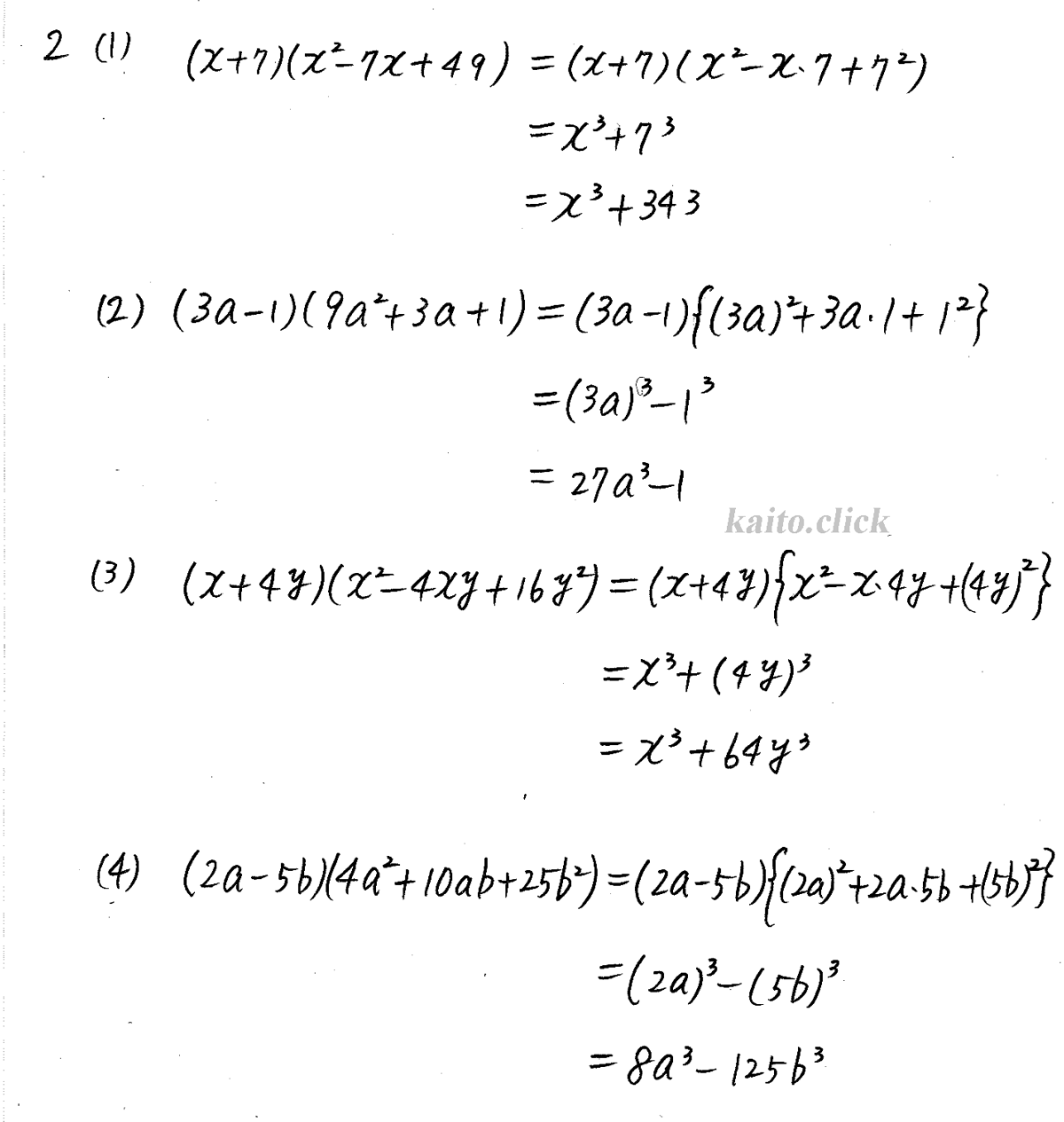



クリアー数学 数2 P6 1 3次式の展開と因数分解
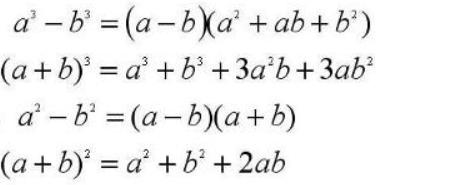



5 4 因式分解 知乎




如何因式分解三次多项式 12 步骤




勉強しよう数学 3次方程式の一般解
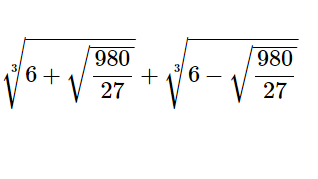



複3次式の因数分解 式 方程式11 数学検定1級の壁




高校数学 文字係数3次方程式が2重解 異なる3実数解をもつ条件 受験の月




一般三次方程式的解 配立方 Youtube




因数分解 発展 三次式の因数分解 Youtube




高次式の因数分解 高次方程式 大学受験の王道
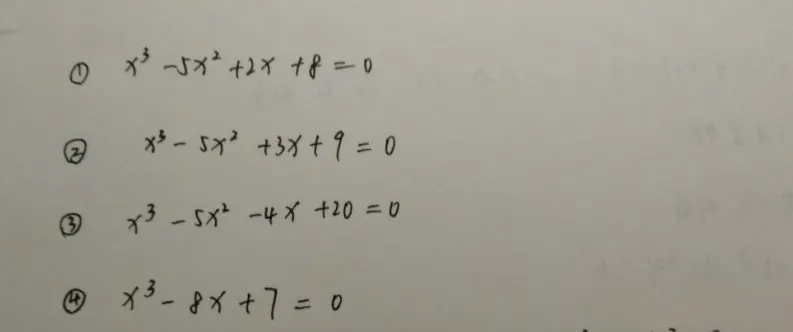



数学技巧 一元三次方程求解 十字交叉法解一元三次方程 个人高中偶然发现的一个数学技巧 知乎




1講 3次式の展開と因数分解 1節 式と計算 問題集 1章 式と証明




如何因式分解三次多项式 12 步骤




二次方程式 因数分解を利用した解き方を例題解説 数スタ




3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す




一元三次方程因式分解拆根 Csdn




数学争议丑闻 三次方程求根公式 光环下的阴影 Youtube




如何因式分解三次多项式 12 步骤




数学 B 3次式の因数分解 広島工業大 関西学院大 北海道医療大 東海大 大学入試数学の考え方と解法




3次方程式まとめ 解き方 因数分解 解と係数の関係 理系ラボ




1講 3次式の展開と因数分解 1節 式と計算 問題集 1章 式と証明




高次式の因数分解 高次方程式 大学受験の王道




19 03 13因式分解法解一元三次方程 哔哩哔哩 Bilibili




高校数学 因数定理と3次式の因数分解 練習編 映像授業のtry It トライイット



中3数学2次方程式2次方程式の解き方因数分解による解き方 Mpg On Vimeo




高次方程式のまとめ 解き方 因数分解 理系ラボ




高中生到熟女都在問一元三 四次方程式怎麼解 註 Medium目前不支援latex 雖然我也不太會用 By Thomas Anderson Medium




3次方因式分解公式 質因式分解 Lecmcw
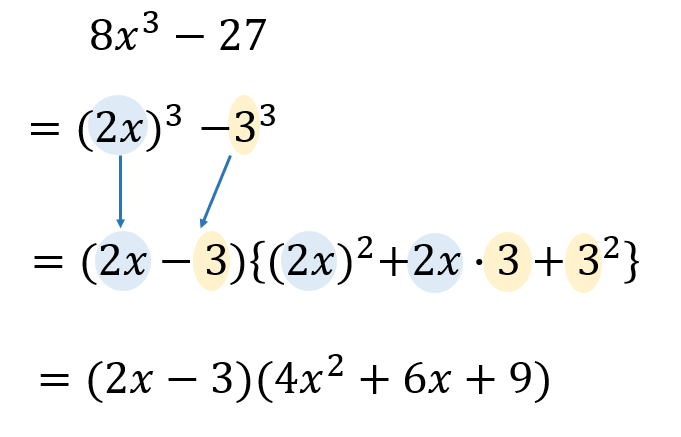



3次式の因数分解 公式とやり方について問題を使って解説 数スタ



三次方程式の解き方を解説 三次式の因数分解の公式など 受験辞典




一元二次方程的解法 解一元二次方程的基本方法 52fmz资讯网



初中数学解一元四次方程 看似有难度 其实通过换元降次就很简单 哔哩哔哩 つロ干杯 Bilibili



3




文字が3つの因数分解 すうがくのいえ
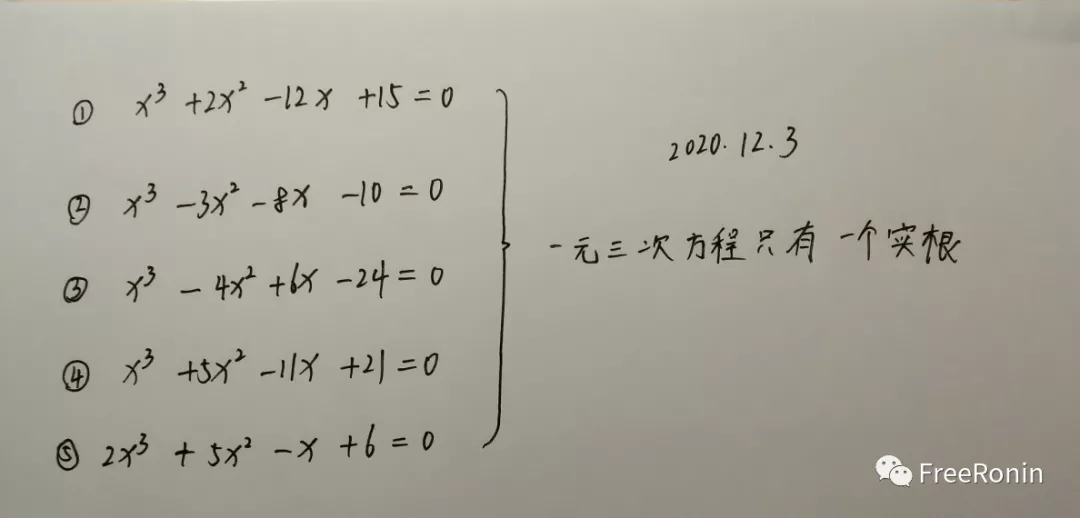



数学技巧 一元三次方程求解 十字交叉法解一元三次方程 个人高中偶然发现的一个数学技巧 知乎



三次因式分解 3次方多项式有什么因式分解的方法举些例子 尚书坊



三次関数とは グラフの書き方 極値や接線の求め方 微分 受験辞典



因式分解之待定係數法 一元三次多項式分解 每日頭條




解高次方程式 Youtube




3次式の因数分解 公式とやり方について問題を使って解説 数スタ



展開の公式 3次式の因数分解をおろそかにしていた私 さんの日記 50代から理数を学ぶ
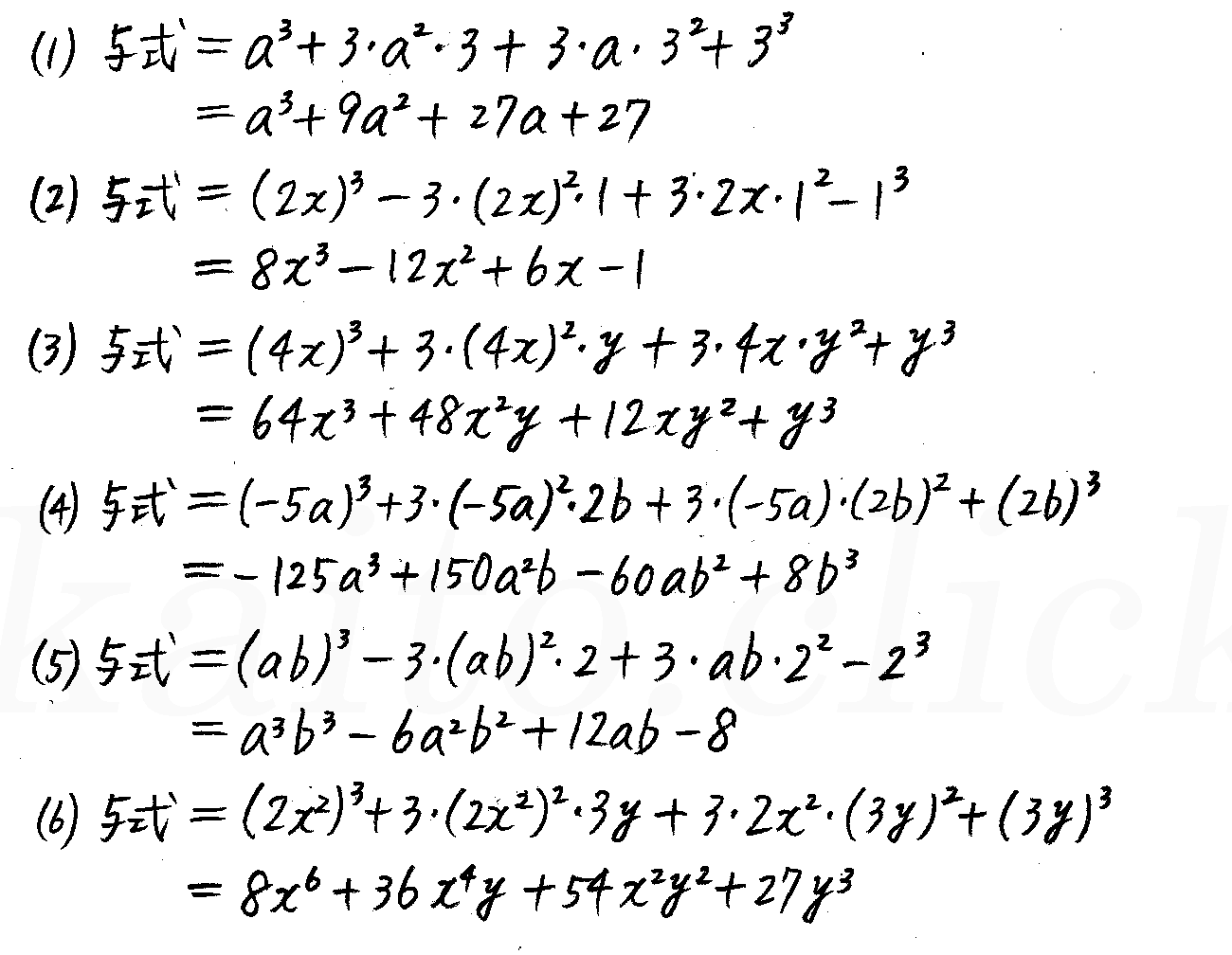



改訂版 4step数学 P6 1 3次式の展開と因数分解




三次函數因式分解計算器factoring Cubic Function Calculator 學校沒有教的數學 學校沒有教的數學
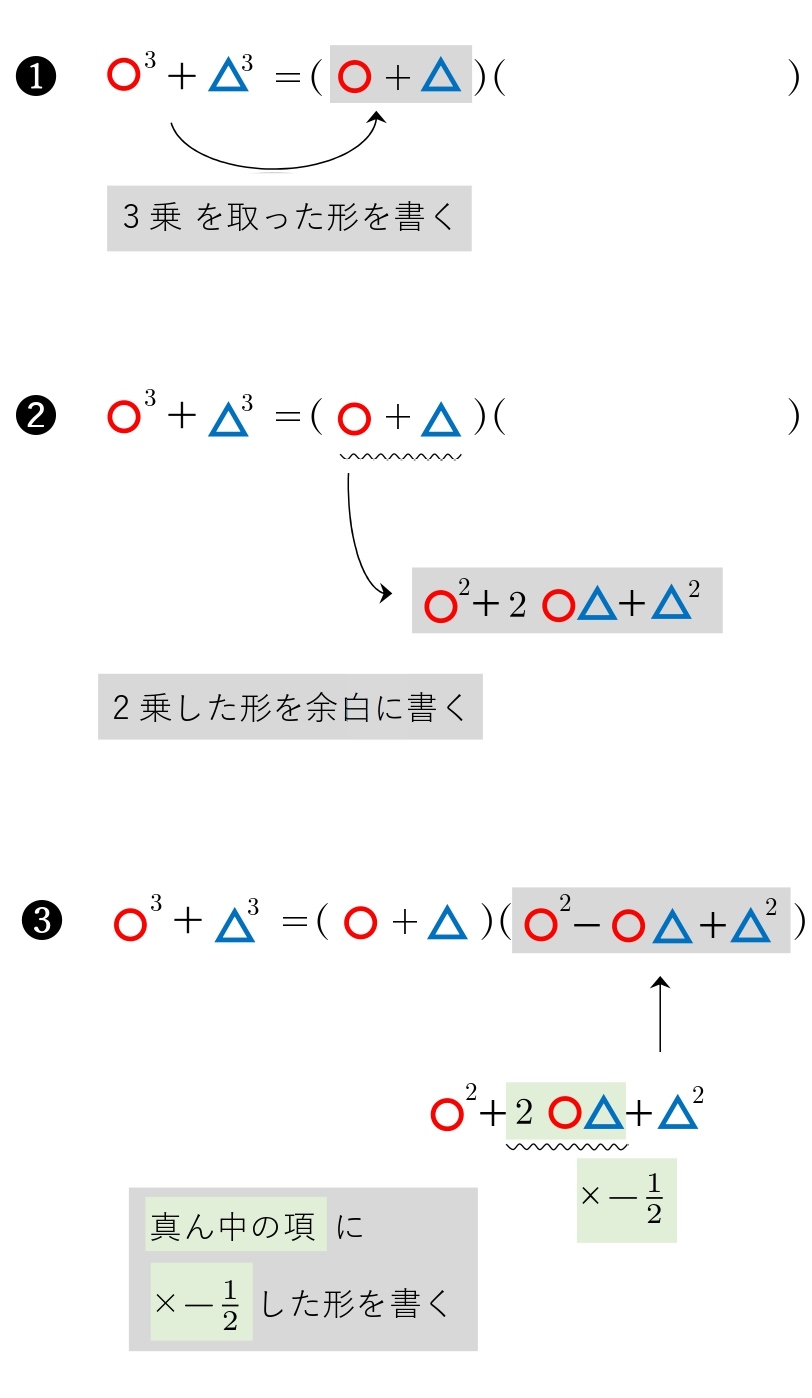



高校数学 3次式の展開 因数分解 公式 覚え方 計算方法 学校よりわかりやすいサイト



因式分解公式
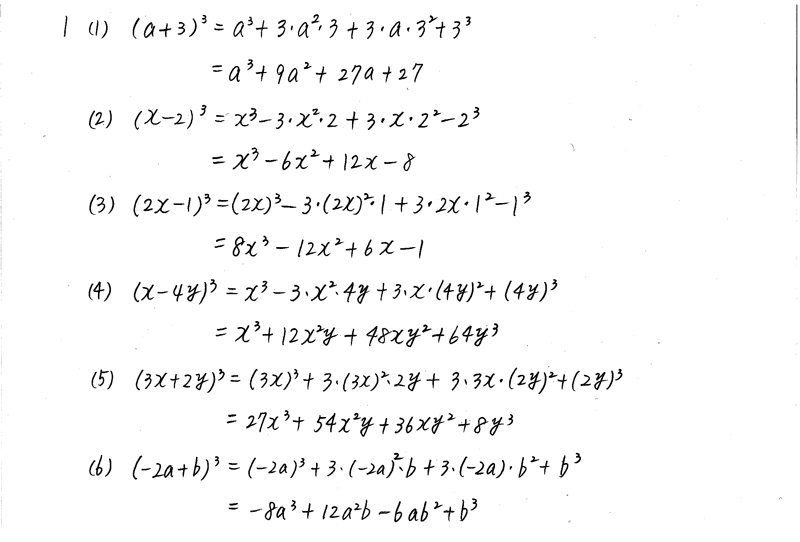



新課程 3trial数学 P6 1 3次式の展開と因数分解



19 03 13因式分解法解一元三次方程 哔哩哔哩 Bilibili




モルヒネ平均バンカー3 次方程式公式 Otope Jp
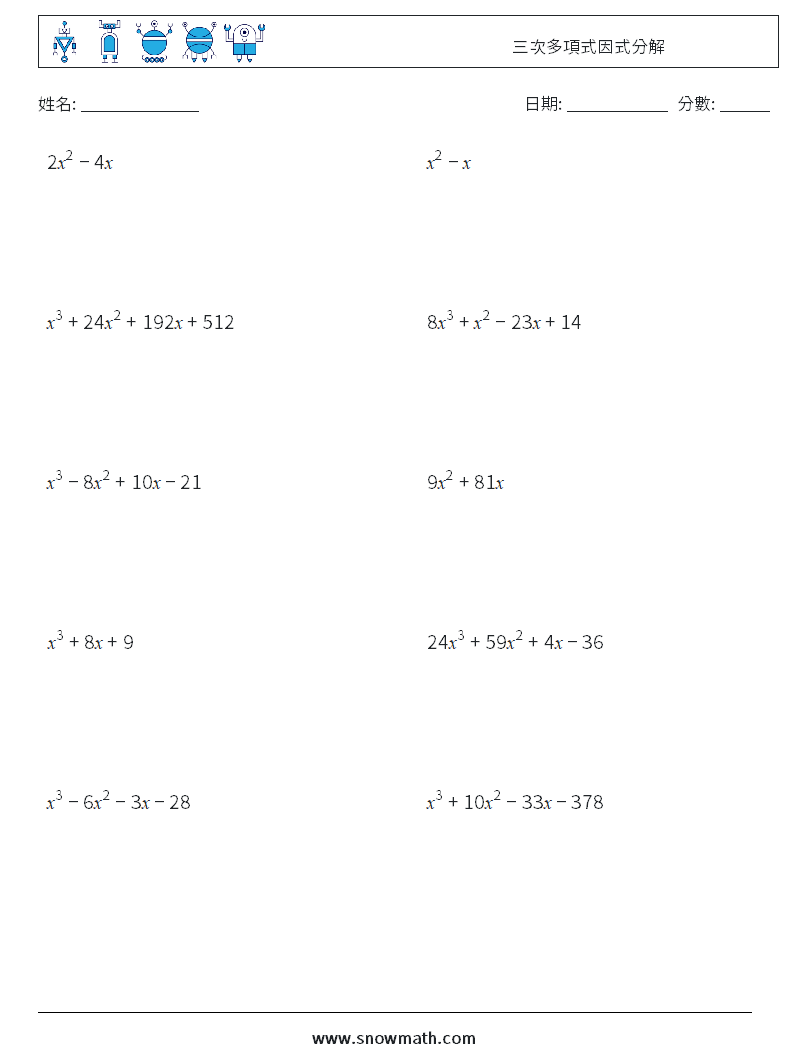



三次多項式因式分解兒童數學練習國小國中數學練習題題庫下載列印 教學學習解答




3次方程式まとめ 解き方 因数分解 解と係数の関係 理系ラボ



三次方程式の解き方を解説 三次式の因数分解の公式など 受験辞典



数学の三次方程式 です このしかくのなかの因数分解を忘れて Yahoo 知恵袋




Download 因数分解 その2 基本images For Free




3次方程式の解の公式 カルダノの公式の歴史 導出 具体例




2 3b觀念01因式分解三次多項式 為什麼我們需要牛頓定理 數學 均一教育平台




高中生到熟女都在問一元三 四次方程式怎麼解 註 Medium目前不支援latex 雖然我也不太會用 By Thomas Anderson Medium
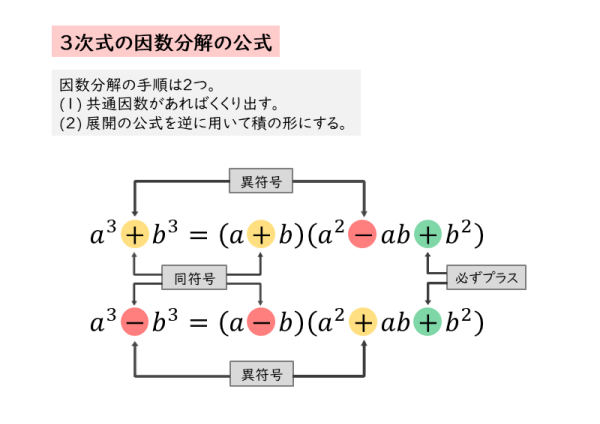



式と証明 3次式の因数分解について 日々是鍛錬 ひびこれたんれん




因式分解一元三次方程技巧 陈木舟的博客 爱代码爱编程
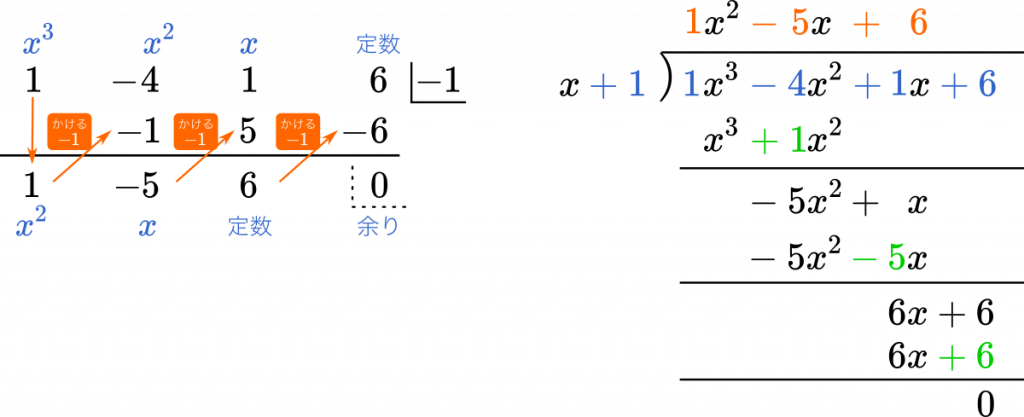



数ii高次方程式 因数定理と組立除法でなぜ因数分解できるのか納得いかない Mm参考書




5次以上の方程式になぜ解の公式が存在しないのか 2 3次方程式の解の公式 準備編 中学でもわかる浪漫数学 Note




19 03 13因式分解法解一元三次方程 哔哩哔哩 Bilibili
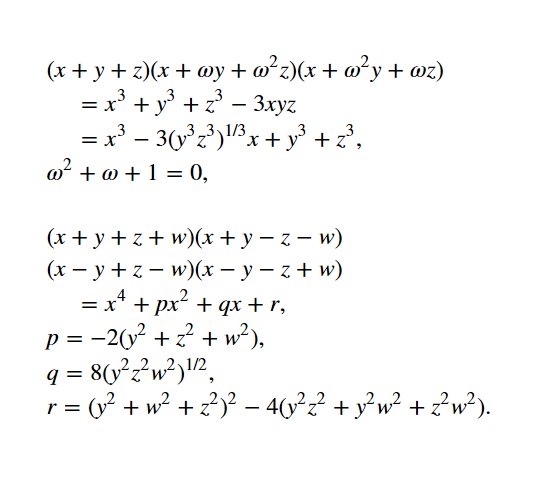



因数分解の公式と3次方程式と4次方程式の解法 Twitter




高中生到熟女都在問一元三 四次方程式怎麼解 註 Medium目前不支援latex 雖然我也不太會用 By Thomas Anderson Medium




因数分解その4 3次式 Youtube




独中数学高一第二章 2 7 一元多项式的因式分解 Uec Mathematics Senior 1 Chapter 2 Youtube




Download 数学 因数分解 Images For Free



求解三次多项式方程儿童数学练习国小国中数学练习题题库下载列印 教学学习解答




高中生到熟女都在問一元三 四次方程式怎麼解 註 Medium目前不支援latex 雖然我也不太會用 By Thomas Anderson Medium




因式分解技巧 二元二次的分解 星空暗流 博客园




3乗の因数分解 展開 公式 理系ラボ




求解三次多項式方程兒童數學練習國小國中數學練習題題庫下載列印 教學學習解答




3次方程式の解と係数の関係 おいしい数学




三次函数 百度百科




3次方程式 見つけにくい因数の見つけ方 怜悧玲瓏 高校数学を天空から俯瞰する




三次方程公式三次方程萬能化簡公式 三次方程因式分解技巧 Uhlwc



2



三次多项式因式分解儿童数学练习国小国中数学练习题题库下载列印 教学学习解答




如何因式分解三次多项式 12 步骤



Studydoctor3次方程式の因数分解 高校数学 Studydoctor



求解三次多项式方程数学练习题7儿童数学练习国小国中数学练习题题库下载列印 教学学习解答
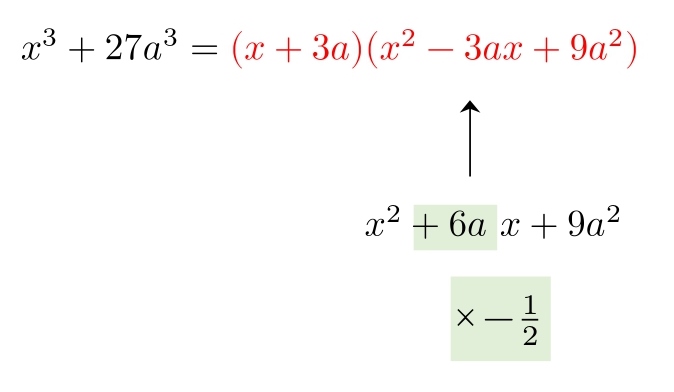



高校数学 3次式の展開 因数分解 公式 覚え方 計算方法 学校よりわかりやすいサイト




3次の因数分解の公式 数学が嫌いなんです



高中生到熟女都在問一元三 四次方程式怎麼解 註 Medium目前不支援latex 雖然我也不太會用 By Thomas Anderson Medium
コメント
コメントを投稿